【中学受験の算数】方陣算の解き方

唐突に😅算数の「方陣算」の解き方を説明してみます。

中学受験の算数。特殊算がいっぱいです。

方陣算もそのひとつ。息子がわかっていると言ったのに、れれれ？な感じになっていたので、やっぱ放置はダメだった😅ってことで、一通り私も復習して一緒に勉強。

方陣算はコツがつかめればすごく簡単に解けるので、得点源になります！

基本問題からちょっとだけ応用まで、ポイントを確認しながら解いていきましょう！方陣算では、碁石とかおはじきとか1円玉を並べたものの数を求めたりします。以下では碁石で統一して説明します。

中学受験の特殊算をぜーんぶ網羅して、すべてわかりやすく解説してくれている『塾技』は中学受験家庭一家に一冊必携です！

 

 

【中学受験】おすすめ算数教材＆問題集６選！

今回は我が家で使用した市販の算数教材をご紹介します。娘、理系志望で算数大好き。なのに成績は凡庸＿|￣|○ しかし、小学生の学力って、戦う必要のない雲の上のあのクラスの方たちを除けばそんなに変わらないも ...

続きを見る

 

方陣のタイプ

方陣のタイプは２つ。

・中実方陣
・中空方陣

中実方陣

中実方陣は、中身の詰まった（穴の開いていない）方陣です。

並んだ碁石の数を聞かれたら単純に縦×横で求められますね。

中空方陣

中空方陣は、中に穴のあいた方陣です。

碁石の数を求めるときには、ちょっと工夫が必要です。

 

問題のタイプ

方陣算の問題で聞かれることは、大まかに３つに分けられます。

・碁石の総数
・周り（もしくは１周分）の碁石の数
・方陣の一辺の碁石の数

これが、中実方陣か中空方陣かで解き方がちょっとだけやり方が変わります。

 

方陣算の解き方　まずはこれを覚えよう

四畳半切り

方陣算で重要になってくるのが、「四畳半切り」。これができたら後は簡単です。

「しじょうはんぎり」ってなんじゃ？！なんだかわからないけど、なんか強そう！（笑）

その四畳半切り（よじょうはんぎりと読んでもいいよ）、こんなやつです。

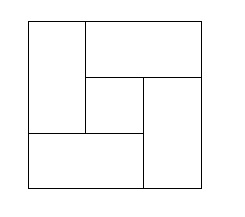
要は四畳半の部屋に畳を敷くときの畳の並べ方！

 

そうなんですよねー。親世代は大丈夫でしょうが、今の小学生が四畳半といって、畳の並べ方がぱっと浮かぶかは疑問ではあります😅。まあしかし、ついでに畳の並べ方も覚えてもらうとして、この図が書けるようにしておきましょう。

うちの息子は不器用なので書けないだろうなぁと思ったら案の定おかしなものを書いていましたのでね、少し出かける間に練習しておくようにいい渡しておきました。

この四畳半切りを使うのは

• 周囲の碁石の数を求めるとき
• 中空方陣の碁石の総数を求めるとき

です。

 

４つのパーツが全部同じ数になるように分けて最後に４をかけて求める方法です。

周囲の碁石の数なら、１列だけなので１辺あたりの碁石の数から１を引いて４倍します。

例えば上の７×７の中実方陣なら、（７－１）×４＝２４　２４個　となります。

中空方陣の場合は、４つに分けたパーツ一つ分に含まれる碁石の数をまず求めて、それを４倍するとすべての碁石の数が求められます。

 

１周分の数は８ずつ増える

方陣の周囲の碁石の数は、四畳半切りで求められると上に書きました。この１周分の碁石の数は外に行くほど増えますよね。

一つ外側にいくごとに碁石の数は「８個ずつ」増えていきます。これを覚えておくと便利です。

 

方陣算はとにかく図を書け

方陣算は簡単そうにみえて、考えているうちにわけがわからなくなりがちです。面積のようにもとめられるのに、求めるのは碁石の数なので、あれ？？みたいにね（笑）。わたしだけかな？！

ですが、図を描くだけで本当に間違いにくくなるし、あっさり解法が見えてきます。

ぜひ面倒くさがらずに図を書く！これを徹底させましょう！

 

例題を解いてみよう！

中実方陣　基本

 

四畳半切りすれば、4等分できますので、4等分した部分の個数（15個）×４で求められます。

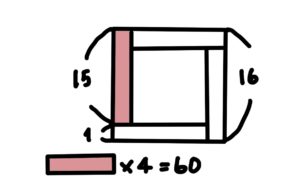
つまり一辺の個数16個から1を引いて、15×４ということになります。いろんなやり方で求めることができますが、四畳半切りを覚えておくと中空方陣や正方形以外の形にも使えて汎用性が高いです。

 

 

１．4畳半切りの一個分の個数を求めます。　48÷4＝12

２．1辺の個数を求めます。上の図のピンクの部分が12個なので、12＋1＝13

３．縦の個数×横の個数で全部の碁石の図を求めます。　13×13＝169

答え　169個

ちなみに平方数は覚えておくと計算が速いので、20×20くらいまで覚えておきましょう！

計算スピードアップの記事にもゴロを書いてます。

【中学受験】計算てどうやったら速くなるの？計算スピードをアップするためにできること

塾のテストのたびに毎回聞いていた、娘の「時間が足りなかった」の言葉。模試だけではありませんよ。4年5年の組分けでもずっとそんな感じでした😭 でもテストで時間が足りなくなって最後に焦って ...

続きを見る

 

 

１．縦横1列ずつ増やしたところにいくつ碁石があるか考えます。　6＋25＝31

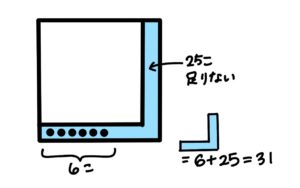
２．増やす前の一辺の碁石の数を求めます。　（31－1）÷2＝15

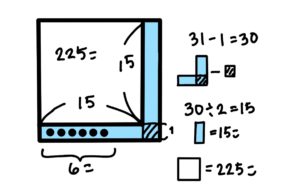
３．余っていた碁石の数を足して、碁石全部の個数を求めます。　15×15＝225　225＋6＝231

答え　231個

 

中空方陣　基本

 

１．四畳半切りにして、四等分した碁石の縦の碁石の数を求める。　15－2＝13

２．四等分したものの１つ分の碁石の数を求める。　13×2＝26

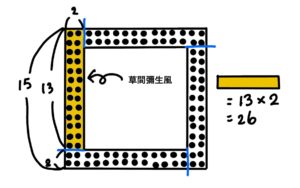
３．4倍する。　26×4＝104

答え　104個

こちらも色んな求め方ができると思いますが、図を描いて四畳半切りをすると一発でわかります👍

 

 

１．外側の個数を4で割って、中空方陣の1辺の個数を求める。　64÷4＝16　16＋1＝17

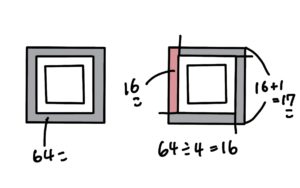
２．四畳半切りしたものの縦の長さを求める。　17－4＝13

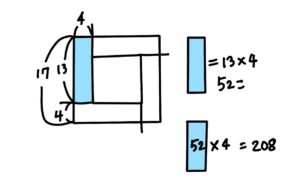
３．四畳半切りの1個分の個数を求める。　13×4＝52

４．4倍する。　52×4＝208

答え　208個

一辺の個数を求めるための図と、中空方陣全部の個数を求める図を分けて描くとわかりやすいです。

 

応用

 

１．一番外側と一番内側の差48を一周ごとに増える碁石の数「8」で割る。　48÷8＝6

２．6回碁石が8ずつ増えているので、並んでいる碁石の列は植木算の要領で1を足す。6＋1＝7

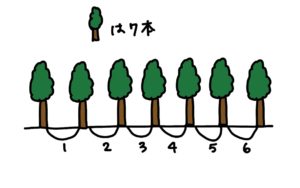
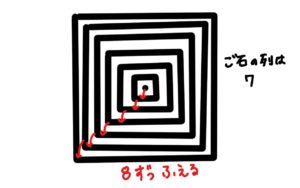
答え　7列

 

まとめ

方陣算の解き方をまとめてみました。集合体恐怖症の方は気持ち悪かったですよね💦スミマセン！

方陣算は図が命。

とりあえず図さえかければ、あとはとってもシンプル。難しい計算もなく簡単にわかってしまうので、方陣算がうーんなお子さんには、とにかく面倒くさがらずに図を描こう！と励ますといいと思います。

うちの息子も面倒くさがって図を描かないので、これさえ書けばすぐ解けるよー！と繰り返し言って聞かせております。

最後にもう一度方陣算のポイントを～。

四畳半切りの概念を持っておくと、四角形でなくても、三角形でもその他の多角形でも解けますよ！

 

【中学受験】おすすめ算数教材＆問題集６選！

今回は我が家で使用した市販の算数教材をご紹介します。娘、理系志望で算数大好き。なのに成績は凡庸＿|￣|○ しかし、小学生の学力って、戦う必要のない雲の上のあのクラスの方たちを除けばそんなに変わらないも ...

続きを見る

【中学受験】ケアレスミス撲滅！算数編

4年生の息子先週の算数は分数でした。最近息子が割り算でよく計算ミスをしているので、そういえば以前読んだケアレスミスの本に割り算を分数でやれば間違いが減るっていうのがあったなぁと思いだしました。 娘の受 ...

続きを見る