塾のテストのたびに毎回聞いていた、娘の「時間が足りなかった」の言葉。
模試だけではありませんよ。4年5年の組分けでもずっとそんな感じでした😭
でもテストで時間が足りなくなって最後に焦って手汗マックスな経験は私だっていっぱいあります。だからこそ、「次がんばれ!」ではなく、具体的な戦略を考えなければと思ったものです。
今回は計算スピードをアップするためにできること、我が家でやったことを書いていきます。
計算スピードをアップしよう
暗記する
算数で暗記って、公式も含め本当はお勧めできないやり方ですが、九九と同じく何度も出てくるものは覚えてしまったほうが絶対いいものもあるのです!
過去問を解くようになってくると、ただでも複雑なのに、解法がわかったらすぐ解けるというのではなく、その後の計算まで面倒というような問題にも遭遇します。学校によってはそういう問題しか出さない、という学校もあるくらいです。
塾の先生でも解きたくないというような、根気のいる、余白が真っ黒になるほど計算が続く、そんな問題も珍しくないのです。
その計算を一行程でも短くするために、絶対に覚えたほうがいいものたちです。
平方数
まずは平方数。現在サピックスに通っている4年生の息子も先生から覚えてくるように言われたようです。
20x20くらいまでは覚えちゃいましょう!
| 11x11=121 | いい、いい、胃にいい |
| 12x12=144 | ワンツー、ワンツー、いっしょ♪ |
| 13x13=169 | いざいざ イチローくん |
| 14x14=196 | いよいよ 一苦労 |
| 15x15=225 | 行こう行こう 続こう! |
| 16x16=256 | 色々 煮込む |
| 17x17=289 | いいな、いいな、2泊~ |
| 18x18=324 | いやいや、3人よ |
| 19x19=361 | 行く行く、寒い! |
| 20x20=400 |
余力があれば30x30まで覚えてもいいかもです。
私は語呂に合わせたへたなイラストを横に描いてトイレに貼っておきました。語呂自体も思い浮かぶ限りおかしなものを使用したほうが忘れにくいので、ぜひできる限りバカバカしいものを考えてみてください。文章で読んだだけでは意味が分からない、あり得ない内容でも、イラストを添えれば、それがシュールなほど効果が高くなります!😁
色付きならさらに忘れにくくなると言われています。
絵が苦手でも大丈夫。絵も下手すぎて面白ければ、印象に残ります😆
それも無理なら、語呂のシチュエーションを説明してあげてください。一度頭に入ってその絵が脳内に浮かべば、忘れにくくなりますから!
三角数 タイルをピラミッド型に並べるやつ
三角数もある程度覚えてしまえば早く答えにたどり着けます。
子供のころよく、「1+2+3+4+5+6+7+8+9+10は??」なんてクイズかなぞなぞ的に問題を子供同士で出し合ったりしませんでした?アレです😆
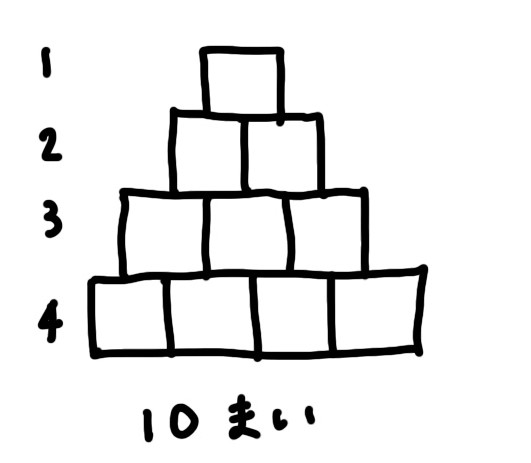
規則性で効いてきます。正方形のタイルを下に行くほど1枚増える感じに並べていく的な問題ありますよね。
うちの息子は全部絵に描いて数えていて、そのうち、スペースがなくなったり雑すぎて線がまがってわけわからなくなってましたけどもね、これ覚えておけば有利に働くこと間違いなしです。

なんでまるおに教えてなかったの!
あ、息子には教えるの忘れてました。
でもね、暗記だけにたよると応用力がつきませんから、あくまで本質を理解して計算で求められるようにしておいてから覚えたほうがいいのです。
それと、平方数はそのまま壁に貼っておけばいいですが、三角数はどんな問題のときに使えるかちょっと説明しておいてあげるほうがいいかもしれません。
| 段数 | タイルの総数 | |
| 1段 | 1 | 1=1 |
| 2段 | 3 | 1+2=3 |
| 3段 | 6 | 1+2+3=6 |
| 4段 | 10 | 1+2+3+4=10 |
| 5段 | 15 | 1+2+3+4+5=15 |
| 6段 | 21 | 1+2+3+4+5+6=21 |
| 7段 | 28 | 1+2+3+4+5+6+7=28 |
| 8段 | 36 | 1+2+3+4+5+6+7+8=36 |
| 9段 | 45 | 1+2+3+4+5+6+7+8+9=45 |
| 10段 | 55 | 1+2+3+4+5+6+7+8+9+10=55 |
| 11段 | 66 | 1+2+3+4+5+6+7+8+9+10+11=66 |
| 12段 | 78 | 1+2+3+4+5+6+7+8+9+10+11+12=78 |
| 13段 | 91 | 1+2+3+4+5+6+7+8+9+10+11+12+13=91 |
| 14段 | 105 | 1+2+3+4+5+6+7+8+9+10+11+12+13+14=105 |
| 15段 | 120 | 1+2+3+4+5+6+7+8+9+10+11+12+13+14+15=120 |
| 16段 | 136 | 1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16=136 |
| 17段 | 153 | 1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17=153 |
| 18段 | 171 | 1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18=171 |
| 19段 | 190 | 1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19=190 |
| 20段 | 210 | 1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19+20=210 |
上の表を壁に貼り付けておいてもいいのですが、その前にこの表自体をお子さんに書いてもらうというのもいいと思っています。書くうちに自然に規則性を見つけ出すと思うからです。
うちの息子のような面倒くさがりは、規則性を見つける前にキレてどこかにいってしまいそうですが💧
素数
100以下の素数は25個です。25個といえば、アルファベットより少ない!
おぼえちゃいましょう♪
2、3、5、7、
11、13、17、19、
23、29、
31、37、
41、43、47、
53、59、
61、67、
71、73、79、
83、89、
97
2以外は、一の位が1とか3とか7とか9ばっかですね。って当たり前か😅
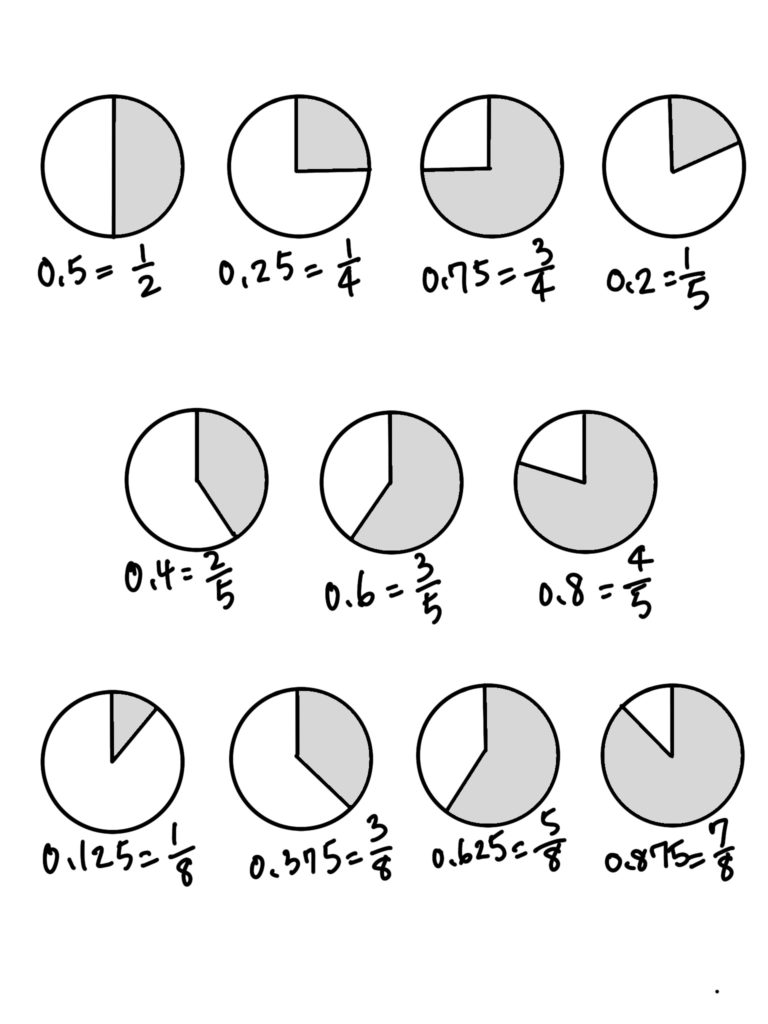
少数と分数の変換
少数と分数の変換もある程度覚えておくと、計算が速くなるだけでなく、時計問題(時間や角度)でも便利です。
角度と分数
円の中心角もパッと分数がでてくると、計算スピードアップにつながります。
もちろんこれも我が家ではテキトーに私がフリーハンドで描いてトイレにはっておきましたよ。

トイレばっか。
180°=1/2、120°=1/3、90°=1/4、72°=1/5、60°=1/6、45°=1/8、40°=1/9、30°=1/12
下の図の緑色の数字は時計の文字盤の数字を書いています。
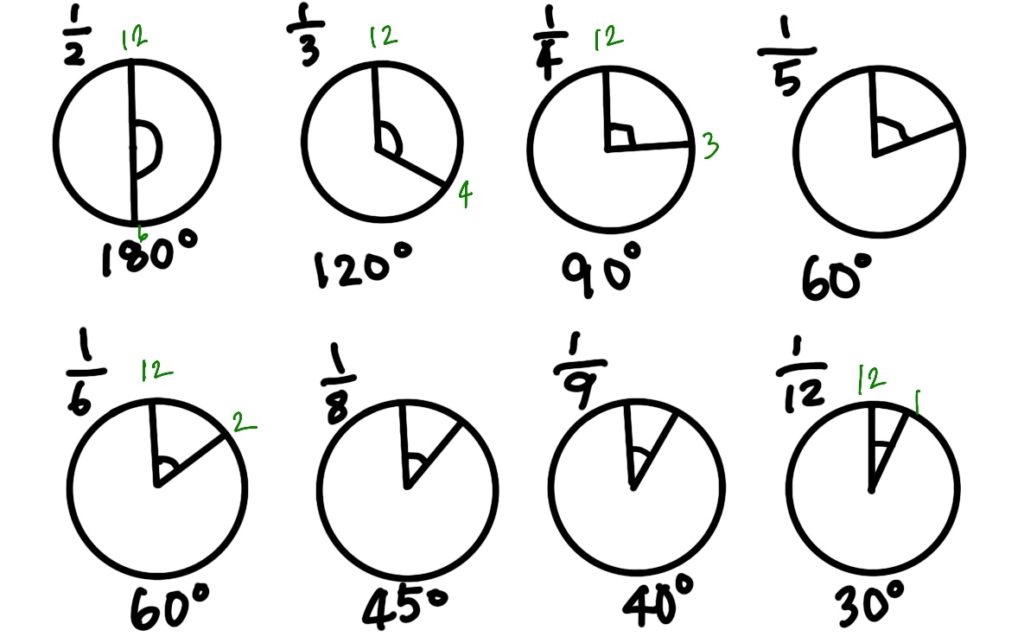
3.14の段
図形問題に円がでてくると、計算が厄介になってきます。円周率はほとんどの学校が「3.14」を使用しています。計算が面倒でも、3.14をかけるとわかっているので先に計算しておけばその手間が省けます!
仮に出題される計算問題を知っていたら、それ、やっておきますよね??!
円周率はそれです。先に計算しておいて試験では取り出すだけにしておけば、試験中に計算しなくて済むんです!
こう考えれば計算をややこしくする憎き円周率にもちょっと親近感❤がわいてくることでしょう😆
| 3.14x1=3.14 | 3.14x6=18.84 | 3.14x11=34.65 | 3.14x16=50.24 |
| 3.14x2=6.28 | 3.14x7=21.98 | 3.14x12=37.68 | 3.14x17=53.38 |
| 3.14x3=9.42 | 3.14x8=25.12 | 3.14x13=40.82 | 3.14x18=56.52 |
| 3.14x4=12.56 | 3.14x9=28.26 | 3.14x14=43.96 | 3.14x25=78.50 |
| 3.14x5=15.70 | 3.14x10=31.40 | 3.14x15=47.10 | 3.14x36=113.04 |
まずは10まで、あとは頻出を太字にしてありますのでそちらを優先して覚えます。
暗算する
初めて算数の家庭教師の先生に来てもらった日に、計算を速くするにはどうしたらいいですか、ときいたら、「暗算する」とおっしゃいました。
裏を返すと、「ひっ算しない」ということのようです。
実はひっ算って、ケアレスミスを引き起こしやすくもある、とも言われています。先生が意味していたのが、ケアレスミスのことではないかもしれないですし、もちろんひっ算しなければならない場面のほうが多いです。
が、上の暗記と同様いくつか覚えると便利なパターンなんかもあるようで、積極的に暗算することを意識して普段から計算するといいみたいです。
うちのこはそろばんもやってないし、私は暗算なんて苦手だから教えようもないし、困ったなと。で早速暗算の本を探しました。
『暗算の達人 驚異の高速暗算テクニック』

この本に一桁目が5の数字の平方数の計算の仕方が載っていました。これは簡単ですぐに覚えられるので、娘も私もすぐに使えるようになりました♪
15x15=225
25x25=625
55x55=3025
85x85=7225
ね!簡単!今私暗算しながら書きましたよ!

「ね!」て言われてもわからないよー!
おけ。
これはですね、一個目の十の位の数字に1を足して、
例えば25x25なら(2+1)x2=3x2=6 これが百の位の数字になります。
あとは5x5=25をその後ろにつけるだけ。6と25をドッキングして625です。
つまりこういうこと↓↓↓
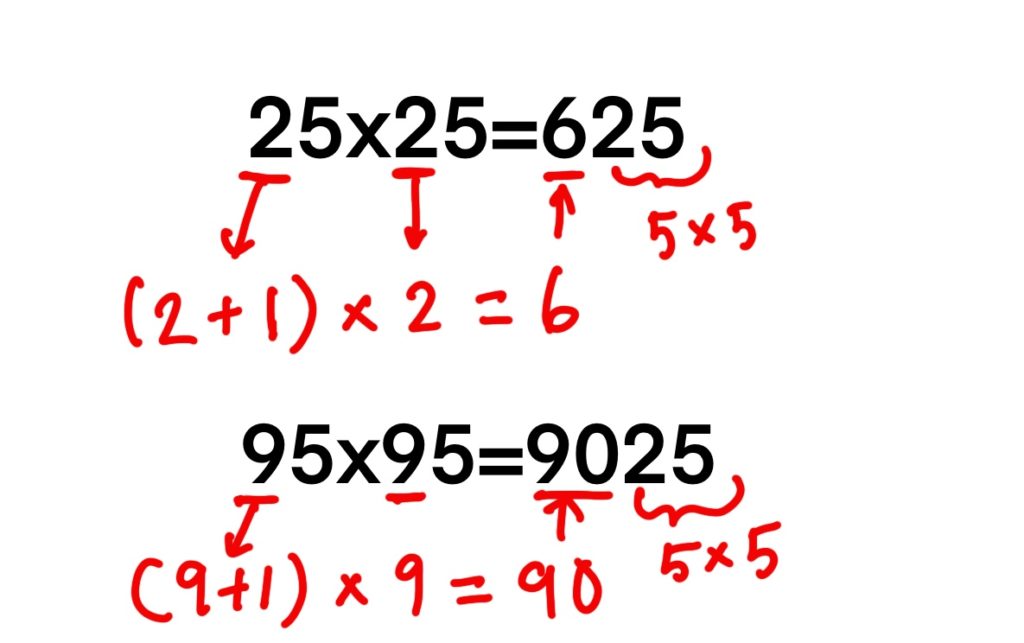
すごい~。娘も実際普段の計算時に使っていますよ!
インド式
そしてずっと昔に夫が買ってきて家にあった『インド式かんたん計算法』ももう一度読んで試してみました。

こちらにも上の5のつく数字の平方数の計算と似たようなのがのっていました。色々あっておもしろく、娘と試してみました。
ひっ算で斜めに掛けるやつ、ネットでたまに見かけますよね。あれも試しましたがなんか微妙。娘は慣れたやり方のほうがいいと普通に戻りました。しかし、大きな数の計算は確かに使えるようになれば速くなるかもです。
すべてでなくても、いくつか使えそうなのがあれば、お子さんの計算力が開花するきっかけになるかも?計算に関しては一生使えるスキルですしね。
マスターしなくても親子で試して、ほんとだ―おもしろー、という程度には盛り上がれました😁
インドでは子供たちが九九どころではない暗算を覚えて(30の段とも99の段とも言われていますが真相は?です)いるなんて聞きますが、どの子も計算激速なんでしょうかね?昔上司がインド人だったので、聞いてみればよかったと今さら後悔しています(笑)。確かにその方はおっそろしく頭のキレる方でしたが。
そういえば昔、『七田式楽しみながら歌って覚える右脳かけ算マスター』という30の段までのかけ算の歌のCDがついた本を買って、子供たちに聞かせていたなぁと思いだしました😂まだ赤ちゃんだった時🤣
インド式の計算ドリルもあるようです!早速買って息子にやらせてみようかな!

毎日欠かさず練習
そして最後はやっぱり、毎日の練習。
ズボラ代表として、本来なら楽してちょちょいと計算スピードがアップする方法をお知らせしたいところですが、どうしてもこればっかりは難しいということです。
算数教材のところにも紹介していますが、量はたくさんでなくても続けることが大事です!うちもバトルが絶えませんが、一緒に頑張りましょう!!
